Erinevus T-testi ja ANOVA vahel
 Share
Share
 T-testi ja ANOVA keskel on õhuke piirjoon, st kui võrrelda vaid kahe rühma populatsiooni keskmist, t-test kasutatakse, kuid kui võrrelda tuleb rohkem kui kahe rühma keskmisi, ANOVA on eelistatud.
T-testi ja ANOVA keskel on õhuke piirjoon, st kui võrrelda vaid kahe rühma populatsiooni keskmist, t-test kasutatakse, kuid kui võrrelda tuleb rohkem kui kahe rühma keskmisi, ANOVA on eelistatud.
T-test ja variatsioonianalüüs, lühendatult ANOVA, on kaks hüpoteesi kontrollimiseks kasutatavat parameetrilist statistilist tehnikat. Kuna need põhinevad ühisel eeldusel, nagu tavaliselt tuleks valimi moodustamiseks valitud populatsioon jagada, dispersiooni homogeensus, andmete juhuvalimine, vaatluste sõltumatus, sõltuva muutuja mõõtmine suhte või intervalli tasemel, tõlgendavad inimesed neid sageli valesti kaks.
Siin on teile tutvustatud artikkel, et mõista t-testi ja ANOVA olulist erinevust.
Sisu: T-test Vs ANOVA
- Võrdlusdiagramm
- Definitsioon
- Peamised erinevused
- Järeldus
Võrdlusdiagramm
| Võrdluse alus | T-test | ANOVA |
|---|---|---|
| Tähendus | T-test on hüpoteesikatse, mida kasutatakse kahe populatsiooni keskmiste võrdlemiseks. | ANOVA on statistiline tehnika, mida kasutatakse enam kui kahe populatsiooni keskmiste võrdlemiseks. |
| Testi statistika | (x ̄-µ) / (s / √n) | Proovi variatsiooni vahel / proovi variatsiooni sees |
T-testi määratlus
T-testi kirjeldatakse kui statistilist testi, mille abil kontrollitakse, kas kahe valimi populatsiooni keskmised erinevad üksteisest suuresti, kasutades t-jaotust, mida kasutatakse siis, kui standardhälve pole teada, ja valimi suurus on väike. See on tööriist, mille abil analüüsida, kas kaks proovi on võetud samast populatsioonist.
Test põhineb t-statistikal, mis eeldab, et muutuja on normaalselt jaotunud (sümmeetriline kellakujuline jaotus) ja keskmine on teada ning populatsiooni dispersioon arvutatakse valimi põhjal.
T-testis toimub nullhüpotees H kujul0: µ (x) = µ (y) alternatiivse hüpoteesi H vastu1: µ (x) ≠ µ (y), kus µ (x) ja µ (y) tähistavad populatsiooni keskmist. T-testi vabadusaste on n1 + n2 - 2
ANOVA määratlus
Variatsioonianalüüs (ANOVA) on statistiline meetod, mida tavaliselt kasutatakse kõigis olukordades, kus tuleb võrrelda rohkem kui kahte populatsiooni keskmist, näiteks saagi saagikust mitmest seemnesordist. See on teadlase jaoks oluline analüüsivahend, mis võimaldab tal testi samaaegselt läbi viia. ANOVA kasutamisel eeldatakse, et valim võetakse normaalselt jaotatud populatsiooni hulgast ja populatsiooni dispersioon on võrdne.
ANOVA-s jagatakse andmestiku variatsioonide kogusumma kahte tüüpi, st juhusele eraldatud summa ja konkreetsetele põhjustele määratud summa. Selle põhiprintsiip on testida populatsioonide keskmiste varieeruvust, hinnates rühmasiseste erinevuste suurust, võrdeliselt rühmadevahelise erinevusega. Valimis on dispersioon tingitud juhuslikest seletamatutest häiretest, samas kui valimi dispersioon võib erinevat käsitlust põhjustada.
Selle tehnika kasutamisel kontrollime nullhüpoteesi (H0), kus kõik populatsiooni keskmised on samad, või alternatiivne hüpotees (H1), milles vähemalt ühe populatsiooni keskmine on erinev.
Peamised erinevused T-testi ja ANOVA vahel
T-testi ja ANOVA olulisi erinevusi käsitletakse üksikasjalikult järgmistes punktides:
- Hüpoteesitesti, mida kasutatakse kahe populatsiooni keskmiste võrdlemiseks, nimetatakse t-testiks. Statistilist tehnikat, mida kasutatakse enam kui kahe populatsiooni keskmiste võrdlemiseks, nimetatakse variatsioonianalüüsiks või ANOVA-ks.
- T-testi testi statistika on:
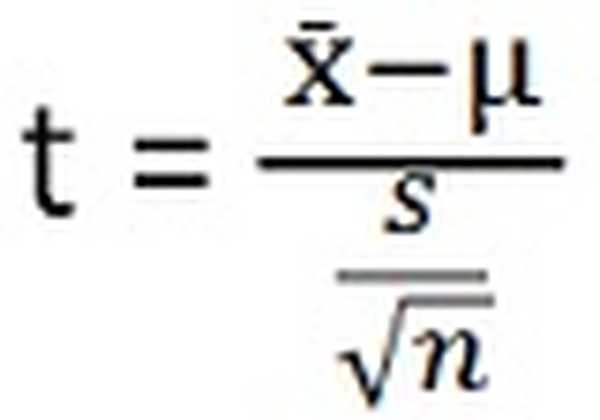 ANOVA testi statistika on:
ANOVA testi statistika on: 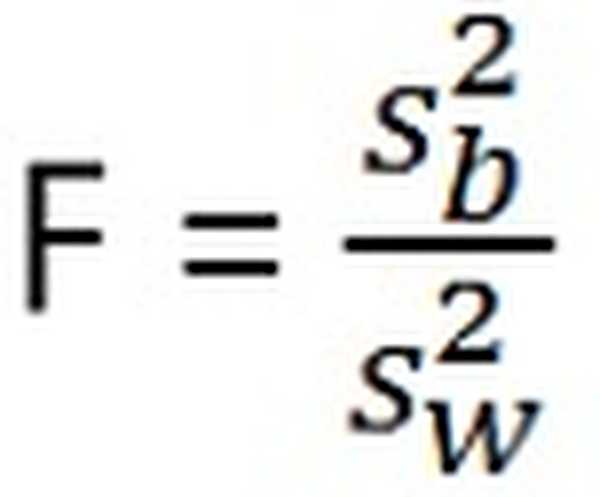
Järeldus
Pärast ülaltoodud punktide ülevaatamist võib öelda, et t-test on ANOVA eritüüp, mida saab kasutada siis, kui meil on ainult kaks populatsiooni, et nende vahendeid võrrelda. Ehkki t-testi kasutamisel võib vigade tõenäosus suureneda, kui peame samaaegselt võrdlema rohkem kui kahte populatsiooni keskmist, kasutatakse seetõttu ANOVA-d
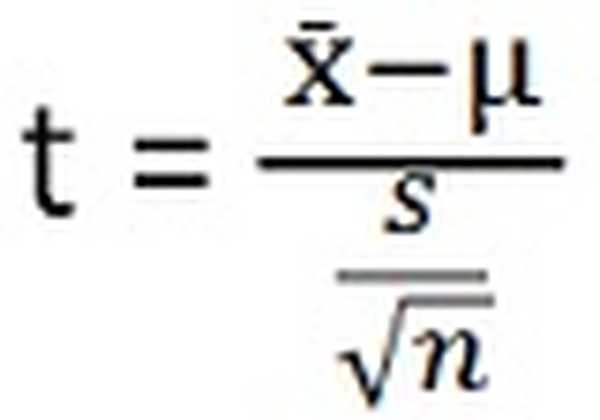 ANOVA testi statistika on:
ANOVA testi statistika on: